kirchoff's law definition and derivation explained

Gustav Kirchhoff, the famous scientist introduced the concept of kirchhoff's law. kirchhoff's law has two state KCl and KVl.

• Kirchhoff's current law (KCL) explains the behavior of current, which flows through a branch of the circuit.
• Kirchhoff"s voltage law (KVL) explains the behavior of voltage, which flows through a closed circuit.

Why we need Kirchhoff's Law?

1. Kirchhoff's law is helpful to understand the complex circuit in electronics.
2. The law is applicable only for closed circuits.
3. Kirchhoff's law is helpful to calculate the current or voltage flowing through the resistance or any equipment connected to the circuit.
4. By using Kirchhoff's law we can find the unknown value such as voltage, current, impedance, etc.

First Law: Kirchhoff's current law or Point law.

Kirchhoff's current law states that "Algebraic sum of current entering the node or junction is equal to the Algebraic sum of current leaving the node or junction, which is also equal to zero".

Proof.

Now look at the circuit in the figure,

Current I1, I2, I3, I4 are meeting at the Point.

Assume that the 

• current (i1 and i3) entering the point is Positive(+ve)
• current (i2 and i4) leaving the point is negative(-ve).

+(+i1)+(+i3)+(-i2)+(-i4)=0

therefore, i1+i3 = i2+i4

By this equation,that Kirchhoff's current law is proved.

Second law: Kirchhoff's voltage law.

Kirchhoff's voltage law states that"In any closed circuit, the total voltage around the loop or circuit is equal to the algebraic sum of voltage drop, which is also equal to zero".

ie, it simply explains that the summation of voltage in a closed loop is equal to zero.

Proof

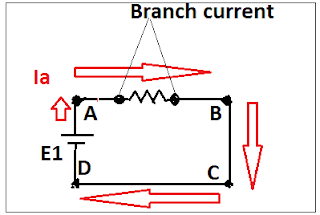
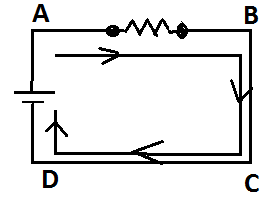
Now considers a closed circuit, with battery and resistor,

Actual current flow from DABC,

The resistor is connected to branch AB. 

Current flows on the branch are called branch current. 

Keep in mind, To find emf voltage around the loop

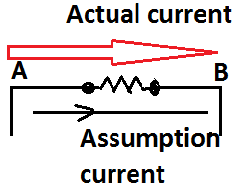
• Compare your assumption current to the actual current flow, if assumption current, flows on +ve side of the battery then we have to consider voltage as +ve. 
• If assumption current flows on -ve side of the battery then we have to consider voltage as -ve.

 My assumption current flow ABCD,

At the battery, my Assumption current flows on -ve side of the battery.

So I took emf or voltage as -ve 

EMF= -V---------------(i) condition

To find a sign of voltage drop, compare assumption current and actual current If its direction is the same then take it as +ve if it is opposite then take it as -ve.

In this circuit assumption current and actual current for the resistor is the same so I took +ve. (Vd=voltage drop)

Voltage drop=Ia*R-------------------(ii)condition

we found both the parameters, according to Kirchhoff's voltage law.

∑ V+∑ IR=0

-v+(+Ia*R)=0

therefore -V = - (Ia*R)